發布者:虹潤集團
在工業生產過程中,人工調節勞動強度大,工作單調,易生差錯,生產效率低,產品質量不易保證。人工調節不能遠離生產設備,因而很難確保安全。此外,現代化生產工藝流程變化速度快、精度要求高,由于人的生理條件所限不能達到控制要求。為此,人們通過實踐,研究設計并制造出各種各樣的儀器、儀表、調節設備、控制裝置等來替代人在調節中的作用,這樣就從人工調節發展到自動調節。
工業生產過程的調節對象范圍很廣,有冶金、化工、石油、電站這四大基礎工業中的調節對象,另外還有輕工、軍工、機械、實驗設備等的調節對象。被調量X(或稱對象的輸出量、被調節參數、被控制參數等)包括的范圍更廣,有四大類:熱工量(溫度T、壓力P、壓差ΔP、流量G、物位H等),成分量(氣體成分A,如含氧O2%、含二氧化碳CO2%等;溶液濃度C,如硫酸H2SO4濃度、氫離子濃度PH值等;物質性質,如濕度,比重,粘度,密度等),電工量(電壓U、電流I、電功率N、電頻率F等)和機械量(重量、厚度,轉速等)。
一、位式調節原理淺釋
(一)二位式調節又稱通斷式控制,是將測量值與設定值相比較之差值經放大處理后,對調節對象作開或關控制的調節。當測量值低于設定值時,儀表輸出“通”的信號,負載因獲得全部能源而升溫;當測量值高于設定值時,儀表輸出“斷”的信號,負載因失去全部能源而降溫;須指出由傳感器-儀表-執行器(閥門或接觸器)-負載(電爐)-傳感器各部分組成的閉環系統在信號的傳遞、處理和調節中都不可避免地存在滯后,故儀表作出調節輸出后,需要一定的時間才能把調節結果再通過傳感器反饋至儀表,在此段滯后時間內,調節對象的溫度仍呈慣性上升或慣性下降,儀表此時處于“失控”階段。能源全部接通和全部關斷二種狀態的交替出現,必然使被控參數有周期性的起伏,形成在設定值上下的震蕩,震蕩的幅度由儀表的回差(又稱開關差)和感溫元件的響應時間、加熱器的熱阻等系統其他部分的特性所決定。這在二位式調節中無法避免。但在空調、農業培植等允許溫度有一定范圍波動的場合,可避免執行器的頻繁動作,反有利于系統的運行。
儀表的回差越小,被控值的波動范圍越小,但調節輸出的動作越頻繁,執行器的壽命縮短。儀表的回差越大,情況則反之,一般把回差值設置在儀表全量程的0.2%-0.5%左右比較合適。
根據上述原理,二位式調節可靠性高而成本低,應用場合十分廣泛。
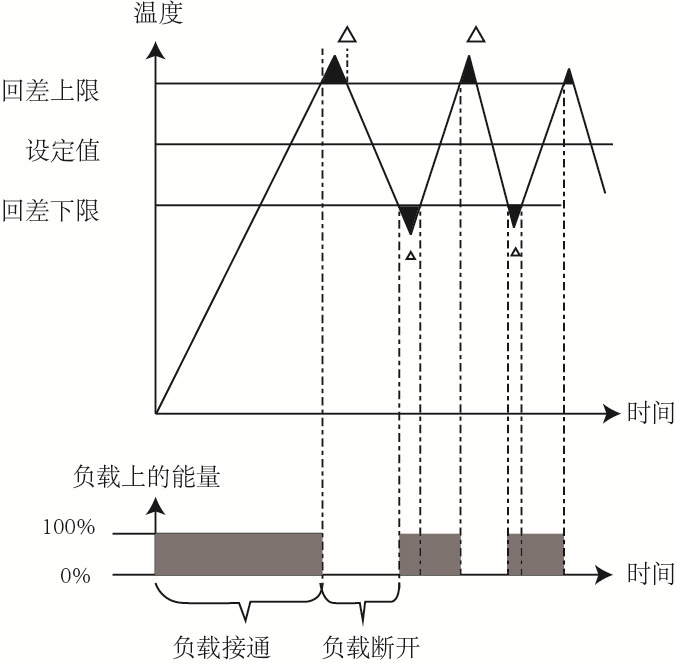
(二)三位式調節是為了克服二位式調節容易產生的升溫速度與溫度對沖量(超調)之間的矛盾而發展的一種調節方式。以電爐加熱為例。三位式調節可以用兩個繼電器的觸點組成“升溫加熱”、“恒溫調節”及“停止加熱”三種輸出狀態。
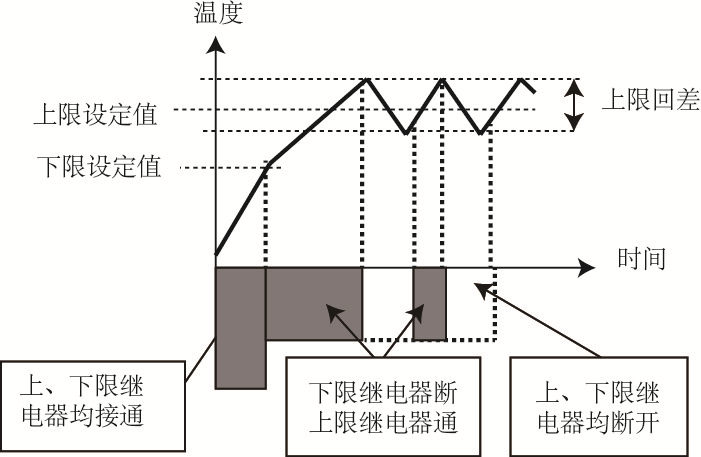
具體實現方法為采用輔助加熱器A和主加熱器B兩組加熱器,當測量值低于下限設定值時,上、下限繼電器均吸合,系統進入“升溫加熱”狀態,此時A、B二組加熱器同時加熱,因此升溫速度較快。
當測量值到達下限設定值,但尚低于上限設定值時,下限繼電器釋放,斷開輔助加熱器A的能源供給,升溫速率隨之下降,系統進入“恒溫加熱”狀態。
當測量值到達上限設定時,下限繼電器仍保持斷開狀態,上限繼電器開始釋放,斷開主加熱器B能源供給。此時由于主輔加熱器均失去能源供給,故溫度逐漸下降,直至降到上限設定回差的下限時,上限繼電器又吸合,接通主加熱器B的能源供給,溫度又逐漸上升,周而復始。由此可見三位式調節比兩位式調節升溫的速度快,進入恒溫調節狀態后溫度的波動小,精度高。
一般情況下,輔助加熱器A的加熱能量為總加熱能量的30%-50%,具體視系統及工況而定。
對不便設置二組加熱器的對象,可以用下限繼電器控制串入負載的電感器或二極管的辦法實現三位式調節,成本降低,且加熱器壽命延長,效果更好。
三位式調節的儀表還可以由下限繼電器承擔加熱調節,而把上限繼電器作超溫時的冷卻輸出或報警輸出,且報警值可由用戶隨意設置,但報警的方式是上限繼電器常閉觸點重新閉合,與正規的報警動作相反,對此須注意。
三位式調節還可用于回差可調的寬中間帶調節方式,其回差約等于上限設定值與下限設定值之差值,在制冷控制系統中應用較多。
(三)連續比例調節
比例的符號為P,凡比例式調節的儀表,均應有一合適(如5%)的比例帶。比例帶的含義是使儀表的輸出從最大改變到最小時,所需輸入信號的變化量占儀表全量程的百分比。比例帶設置得越小,相等的輸入信號變化量可使輸出有更大的改變,反之亦然。
比例帶的作用是使儀表的調節輸出與設定偏差之間有一段逆向的、幾近線性特性的調節區域,在比例帶內,輸入信號的連續增加將使儀表的調節輸出成比例地連續下降,直至輸入增加到比例帶的上限值時,儀表的輸出降低至零。連續調節儀表的輸出方式一般可分為可控硅移相觸發方式和可逆電機驅動電感式調節器方式。
(四)時間比例調節
與上述連續比例式調節相比,時間比例式調節的差別在于其對負載的調節是用脈寬調制方式,以改變單位時間(即周期)內平均加熱功率的方式來實現的。如果一個1000瓦的電爐在30秒鐘周期內通電15秒鐘,斷電15秒鐘,那么在這個周期內,電爐實際得到的加熱功率為50%,即500瓦。以此類推,就可以用簡單的繼電器觸點通與斷之間的時間比值,即用改變“接通”與“關斷”二者占空比的辦法,模擬輸出具有相當分辨率的連續量。由于多數情況下被控對象有較大的熱容量,幾十秒鐘的通斷周期不會表現在被控對象的溫度速變上,因此有很寬的應用范圍。時間比例調節故又稱作斷續式比例調節。
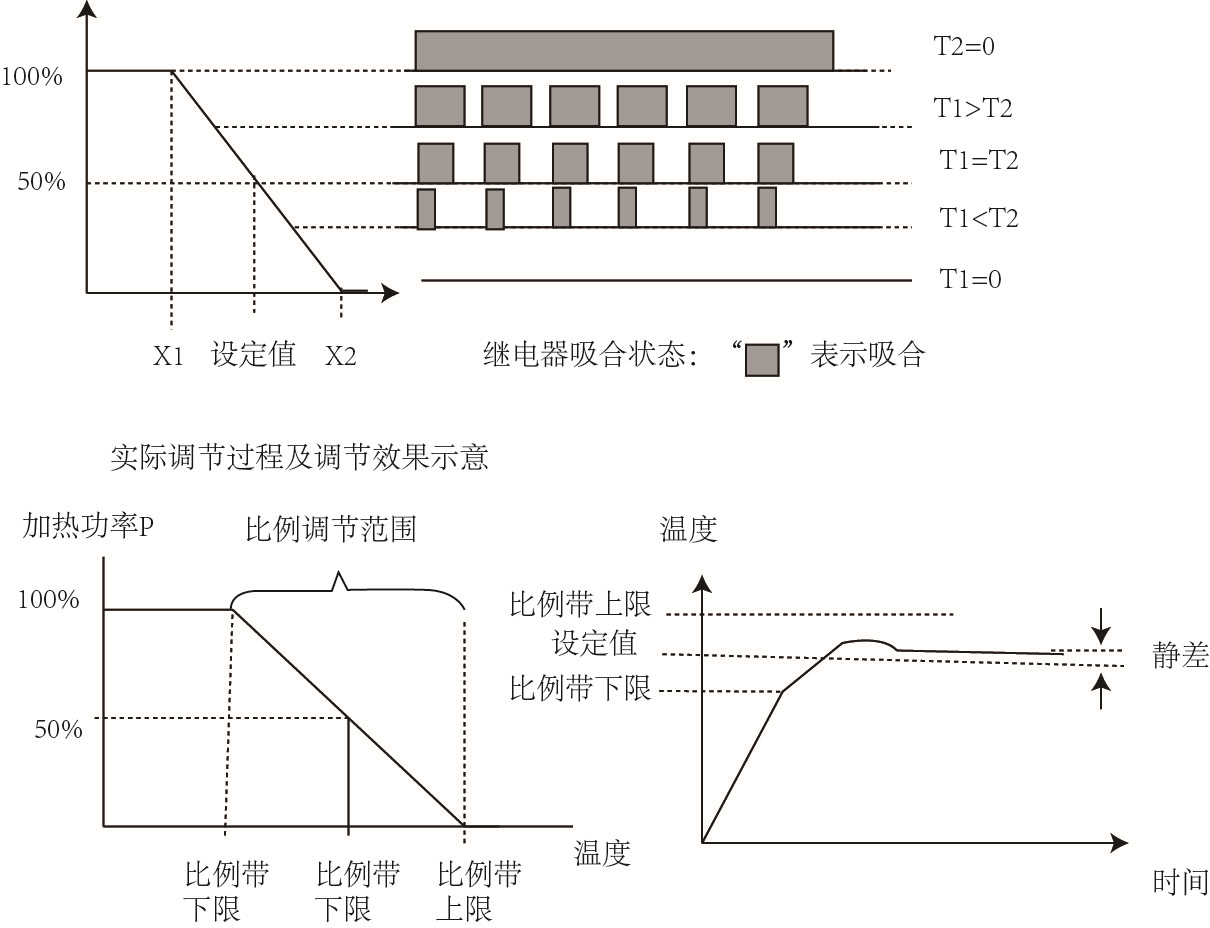 時間比例調節的基本原理:當實際溫度進入儀表的下比例帶時,繼電器即開始周期性地釋放、吸合,靠改變吸與放的時間之比值來改變加熱負載上的平均加熱功率,從而改變溫度的目的。吸放的時間同設定值與測量值的偏差成正比,即偏差越大,單位時間(即吸放周期T)內吸合時間越長,反之越短;當偏差為零時,吸放為等周期,而出現負偏差時,吸合時間比釋放時間短,直至測量值到達比例帶上限,繼電器不再吸合,負載上無輸出。
時間比例調節的基本原理:當實際溫度進入儀表的下比例帶時,繼電器即開始周期性地釋放、吸合,靠改變吸與放的時間之比值來改變加熱負載上的平均加熱功率,從而改變溫度的目的。吸放的時間同設定值與測量值的偏差成正比,即偏差越大,單位時間(即吸放周期T)內吸合時間越長,反之越短;當偏差為零時,吸放為等周期,而出現負偏差時,吸合時間比釋放時間短,直至測量值到達比例帶上限,繼電器不再吸合,負載上無輸出。
繼電器吸合時間T1和釋放時間T2之和為時間比例的周期。而吸合時間T1與周期T之比為時間比值。
與位式調節相比,時間比例式調節對負載的調節是用由偏差決定,連續改變輸出量的大小這一方式去實現的,因此調節結果的波動較小。在有擾動時,被控對象能很快趨向平穩。在比例帶值合適的情況下,不會產生持續的振蕩現象。
比例調節的靜差:比例或時間比例調節在系統穩定時,其實際溫度值與設置溫度值之間有時會有一個偏差,即調節的結果值與設置的目標值之間有一差值,專業上稱之為“靜差”,靜差一般為數攝氏度,可正可負。靜差的大小和方向取決于全輸出時加熱功率的高低、環境溫度或電網電壓的改變和比例帶的大小等各種原因。
二、PID 控 制 算 式
比例、積分、微分控制(簡稱PID控制)是過程控制中應用最廣泛的一種控制規律。1868年麥克斯韋發表了“論調速器”闡述了控制理論基礎。1936年,在此基礎上,ASTRON發表了著名的“PID”調節理論。最優控制理論可以證明,PID控制能滿足相當多工業對象的控制要求。所以,它至今仍然是一種最基本的控制方式。


一個典型的PID單回路控制系統,C是被控參數,R是C的給定值。
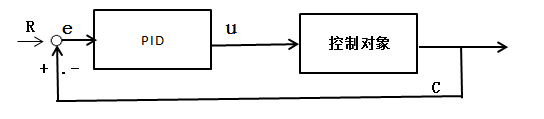

1.調節器的特性
調節器的調節規律或稱調節器的特性。第一種稱為比例調節規律,第二種稱為積分調節規律,第三種稱為微分調節規律。此外就是比例加積分,比例加微分以及比例加積分加微分調節規律。這些調節規律的微積分方程式、在階躍(即訊號一下子)輸入下的輸出時間特性以及傳遞函數等。
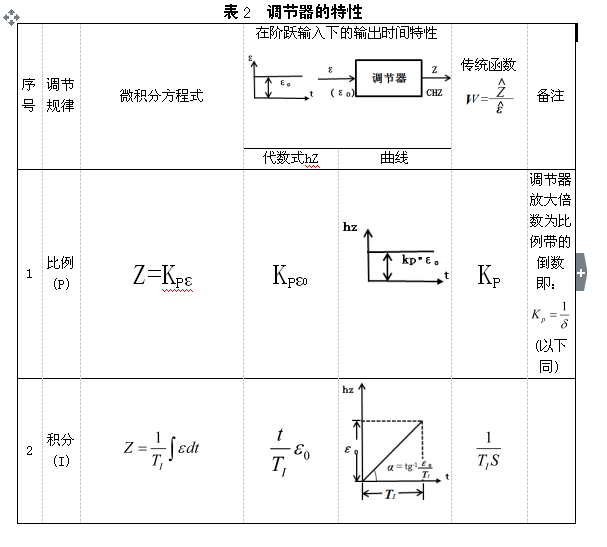


PID算式有兩種基本類型—完全微分型(即理想微分型)與不完全微分型(即實際微分型),根據所采用的計算機的不同輸出部件,兩種類型的算式又各有三種不同的型式,即位置型算式,增量型算式和速度型算式。
(1)位置型算式
智能PID調節器經PID運算,其輸出信號值與調節閥門的開度一一對應。
(2)增量型算式
智能PID調節器經PID運算,指明執行機構所需的相對改變量。計算機的輸出增量為前后兩次采樣所計算的位置值之差。
(3)速度型算式
速度型算式是指智能PID調節器的輸出信號值與調節閥門開度的變化率一一對應,如指明直流伺服電機的轉動速度。
(一)完全微分型算式與不完全微分型算式
一臺智能PID調節器中,要實現所描述的運算是相當困難的,這主要是完全微分項難以制作,因此,在實際控制系統中,采用的微分項往往都是不完全型的。
另一方面,在智能PID調節器中,CPU對每條回路輸出的時間是短暫的,而驅動步進電機走步則需要一定的時間。這樣,如果經過計算得到一個輸出值較大,在智能PID調節器輸出的短暫時間內,步進電機將完成不了這種走步的要求,從而不能實現原來的控制要求。也就是說,由于輸出通道的限制,在被控變量變化較大、并且微分作用Td較大時,雖然計算得了較大的,但是控制作用并沒有較大的變化,從而把微分作用限制住了。這說明,從控制要求的角度來說,希望把過大的微分作用能逐步、平滑地輸出,這樣,能使微分作用真正起作用,從而達到改善控制質量的要求。這就提出了如何實現不完全微分的問題。智能PID調節器的完全微分型式


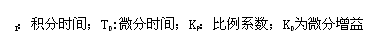
(二)兩類算式的比較和幾點看法
(1)從上面介紹可以看出,完全微分型算式比較簡單。
(2)完全微分型算式調節性能不好,因為完全微分型算式的微分作用在調節過程中受到抑制,不利于按偏差的趨勢進行調節(數學上可以嚴格地予以證明,這里從略),這個缺點是相當嚴重的,許多智能PID調節器調節品質不如常規模擬系統,原因便在于此。而采用不完全微分型算式,便可以避免此缺點,從而大大地改善調節品質。
(3)完全微分型算式與不完全微分型算式的常數,均需事先離線算好,一般智能PID調節器配有相應的子程序,以實現這些常數的離線計算。
(4)這些算式中,增量型算式是最基本的。鑒于國內目前所采用的 對過程變量PV值進行“微分先行”的運算,這種方式對輸出的擾動較小。也有采用比例運算僅對PV進行的“比例先行”方式,這種方式對偏差的響應速度較快。而它們都屬于增量型保持器,所以智能PID調節器算式以增量型為基礎是有實際意義的。
(5)增量型算式轉化成其它型算式是相當容易的。
(6)采用完全微分型算式,計算值容易超出界限,引起溢出停機。這是由于算式在計算第一周期時微分效果相當強的緣故。因此,如采用完全微分型算式,則簡易算式應附加輸出增量限幅部分,否則系統難于正常工作。
(7)綜上所述,雖然完全微分型算式比較簡單,但從滿足調節品質指標方面來看,不完全微分型算式具有更多的優點。從國外的發展趨勢以及據外國專家來華進行技術交流的資料介紹,智能PID調節器越來越傾向于采用不完全微分型算式,并作成許多種偽硬件功能塊(每個功能塊可完成一個控制算式,目前已形成60余種)。因此,在智能PID調節器中,我們建議以采用不完全微分型算式為宜。
(三)編制控制算式子程序框圖的幾點說明
(1)抗積分飽和與限幅
眾所周知,積分的作用可以消除控制系統的殘余偏差。但它也有一個付作用,即在偏差沒有消除以前,它會使計算輸出值一直向兩個極端位置變化,使輸出信號超出正常信號的運行范圍,進入深飽和區。一旦偏差小時,輸出從深飽和區退出需要相當長的時間,這會惡化調節品質。另外,輸出趨于兩個極端,也容易使執行機構頻繁動作振蕩磨損。為避免由于積分飽和現象或其它因素(如過強的微分作用)引起輸出超過執行機構的信號范圍,經常用閥位反饋的方法,在被控參數讀入的同時,把閥位信號也采樣讀入。這樣,計算機就可以知道,閥門尚有多少余量可以調節。但對非線性調節閥要作適當校正。
(2)防止積分極限環的產生
智能PID調節器控制具有較高的控制精度,只要系統的偏差大于其精度范圍,智能PID調節器就要不斷進行控制,改變執行機構的位置。為防止控制過程產生極限環,對智能PID調節器輸出增加一個判斷條件,如果是預先制定一個相當小的常數,即所謂不靈敏區,則智能PID調節器不輸出。
(3)PID參數的選取:如果選用的PID參數不合適,PID調節的結果很可能比二位式調節的結果還差,例如產生幅度很大的連續振蕩,產生長期不能消除的靜差,或者是在系統受擾動后不能盡快復原等等,因此,根據被控對象的工藝過程選取合適的PID參數,是用好智能PID調節器儀表的關鍵點。
(4)PID參數人工整定方法:PID參數的設置情況直接影響系統的調節結果。人工整定PID參數,最簡單實用的辦法是使用“鄰界比例度法”來確定PID參數。具體方法是:將系統接成閉環,關掉I、D(即將參數積分時間I和微分時間D均設置為0),多次調節比例帶P值的大小,使系統剛剛產生振蕩,記錄此時的比例帶參數(XP1)及振蕩周期時間(T),則正確的PID參數可以從表中計算出來(以恒溫調節系統為例說明)。
根據比例帶XP1和振蕩周期T,查表后計算出合適的比例帶、積分時間、微分時間三個參數的具體數值,再按儀表的設置步驟鍵入PID參數并稍作微調即可。
概括地說,比例帶P設置的數值越大,系統越不會發生振蕩,靜差也越大;積分時間I設置的數值越大,積分的作用越不明顯,消除靜差所需的時間也越長,系統越不會發生振蕩;微分時間D設置的數值越小,對比例帶和積分的作用越小,系統越不會發生振蕩,但系統的響應速度也變得遲鈍。積分的作用是使系統趨向穩定,而微分的作用是抑制超調,但會使系統趨向不穩定,微分與積分配合得當,就可獲得盡快而穩定的調節過程。
一般建議:初次運行先以儀表出廠時已設置的PID參數為基礎,如發現系統一直在設定值上下產生非衰減性的振蕩,可逐次把比例帶P或積分時間I的數值增大三分之一左右,直至穩定。反之如發現系統的靜差消除過慢,可減小比例帶P的數值或積分時間I的數值,直至穩定。如發現系統抗擾動的能力不夠,可適當增強微分的作用,即適當加大微分時間。
在一些工況固定的場合,只選用儀表的比例P和積分I功能,而把微分D功能關掉(設置為0),反能取得理想的調節效果。
(5)自整定控制的基本原理
比例-積分-微分控制器或叫“PID回路”事實上作為工業反饋控制方面的標準方法已經超過95年了,但是使用它們并不簡單。為了使PID回路工作到最佳狀態,它們必須在一開始就進行整定以適應每種應用場合。
“自動整定”控制器可以通過自動地響應請求以生成合適的整定參數來完成整定。當控制功能失效時,操作人員只需要按動“自整定”這個按鈕并觀察控制器的整定功能對過程進行操作,直到有足夠多的符合過程自身特性的輸入/輸出數據。大多數自動整定技術就是簡單地模仿一位有經驗的控制工程師在第一次將回路連線時所做的事情。
自整定方法有好多種,如利用微處理器生成M序列偽隨機信號測取對象脈沖反應函數;用最小2乘法在線遞推識別;用優選法在線修改*K p、*T i、*T d等。但前兩種方法占機容量較多,而一般微處理器運算速度較低,內存也有限;后一種方法要在好幾個過渡過程結束后才能完成,不甚及時。
根據筆者以前工作中嘗試過的溫度控制對象自整定方法介紹如下。
(1)開關階躍響應PID參數自整定
這是一種開環整定方法,即利用系統廣義過程的階躍響應特性曲線對調節器參數進行整定。具體做法是:先使系統處于開環狀態。在執行單元輸入端施加一個階躍信號,這個階躍信號的幅度以不影響系統的安全運行限制。記錄下過程量的變化值。根據這個階躍響應曲線將廣義被控過程的傳遞函數近似表示如下:
對于有自衡能力的廣義過程(因為控制對象為加熱爐),傳遞函數可寫為:
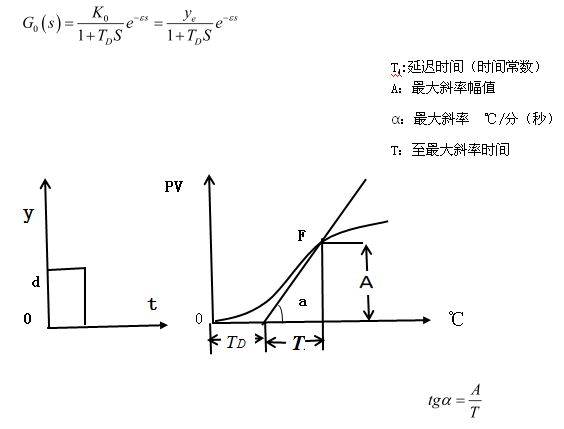
我們通過大量試驗,可以得到,P=Td×最大斜率×輸入幅度/滿量程×100% Ti=0.4×Td TD=0.4/Td
自整定調試試驗結束時,儀表即自動切換到PID控制。
以上經驗數值可能還需要在實際過程中進行修正。
(2)繼電振蕩PID參數自整定方法
1984年,K.J.Astrom提出了在繼電反饋下觀測被控過程的極限環振蕩自整定方法。在自整定調節期間,繼電控制使被控過程產生極限環振蕩,由振蕩曲線可以得到動態過程數學模型的特征參數Tu和Ku,再利用Z-N整定公式計算PID參數。調節過程結束后,系統切換到PID控制。該方法大量節省了技術人員的工作量和調試時間,并且比手動操作有效和可靠,被許多實用的工業控制器所采用。
實用的基于繼電振蕩的PID參數自整定算法的控制過程曲線,該自整定過程至少需要滿量程階躍峰值時間加近兩個振蕩周期,相比基于開環階躍響應的PID參數自整定算法整定時間大大延長。并且被控過程將長時間處于等幅振蕩狀態,這對于許多被控過程和執行器是不允許的。一旦反饋控制功能啟動后,整定功能就可以給出一套P、I和D的整定參數并得到理想的閉環回路行為。因為整定和控制功能是同時進行操作的。控制器必須持續地保持過程變量在規定范圍內,因此它必須試著了解過程變量是如何對控制量進行反作用的。
不幸的是,這些功能都是相互對立的。保持過程變量穩定就會削弱對于過程行為有用的整定功能,反之,模擬整個過程可以了解對控制量如何反應會減弱控制功能。
而幸運的是,總有幾次當控制量和過程變量無論如何波動的時候,閉環回路運行的依然正常,而且大多數的自整定器被設計成可以利用該情況。
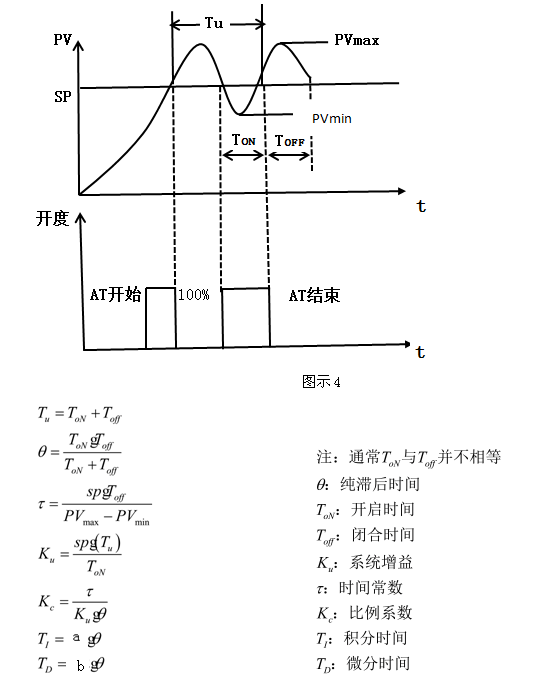
A、B:依據不同溫度控制對象決定的系數
注:John Ziegler和Nathaniel Nichols發明了著名的回路整定技術使得PID算法在所有應用在工業領域內的反饋控制策略中是最常用的。Ziegler-Nichols整定技術是1942年第一次發表出來,直到現在還被廣泛地應用著。
經過許多年的發展,Zigeler-Nichols方法已經發展成為一種參數設定中,處于經驗和計算法之間的中間方法。這種方法可以為控制器確定非常精確的參數,在此之后也可以進行微調。
Ziegler-Nichols方法分為兩步:
構建閉環控制回路,確定穩定極限。
根據公式計算控制器參數。
整定原則
自整定過程結束時,PID參數由自整定算法計算得出。計算PID參數的公式基于增益和過程滯后時間與響應時間的比例。考慮到魯棒性,算法必須在不失穩定性的條件下支持增益與時間常數變化。
(6)調節系統的品質指標
1.目前描述自動調節系統的具體品質指標是在承受階躍形式擾動后被調量過渡過程的一些參數和形態。這些參數有以下幾項:
(1)無差度或穩態誤差ε;
(2)超調量σ%,定值調節系統: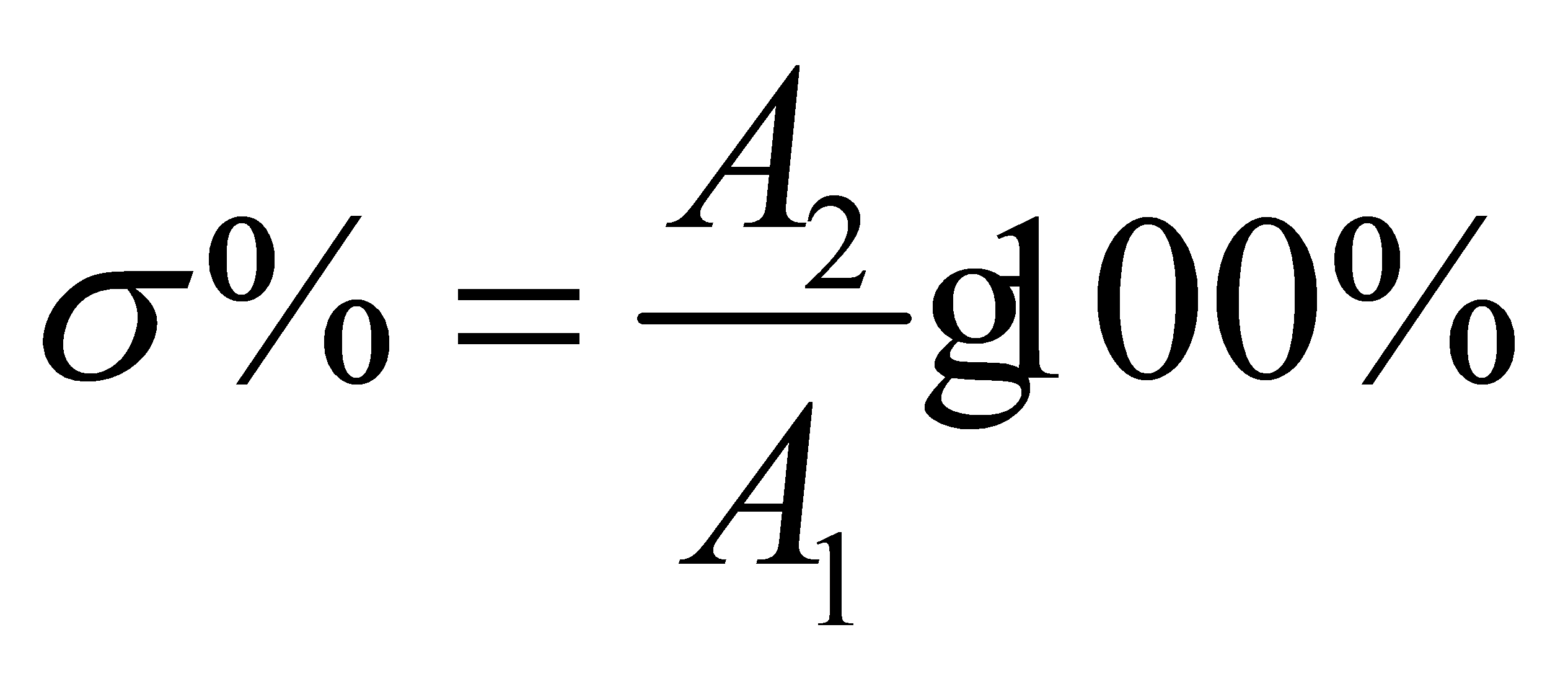 和隨動調節系統;
和隨動調節系統;
圖1(a) 定值調節系統在階躍擾動作用下被調量的波動過程
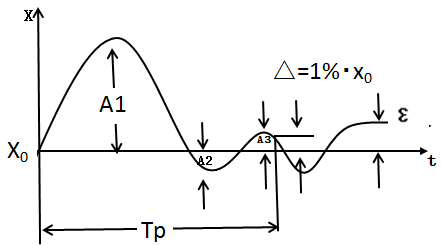
圖1(b) 隨動調節系統在階躍擾動作用下被調量的波動過程
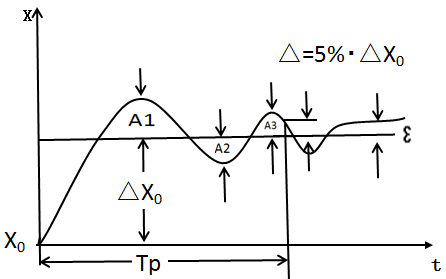
(3)調節時間Tp;
(4)振蕩數X;
(5)衰減度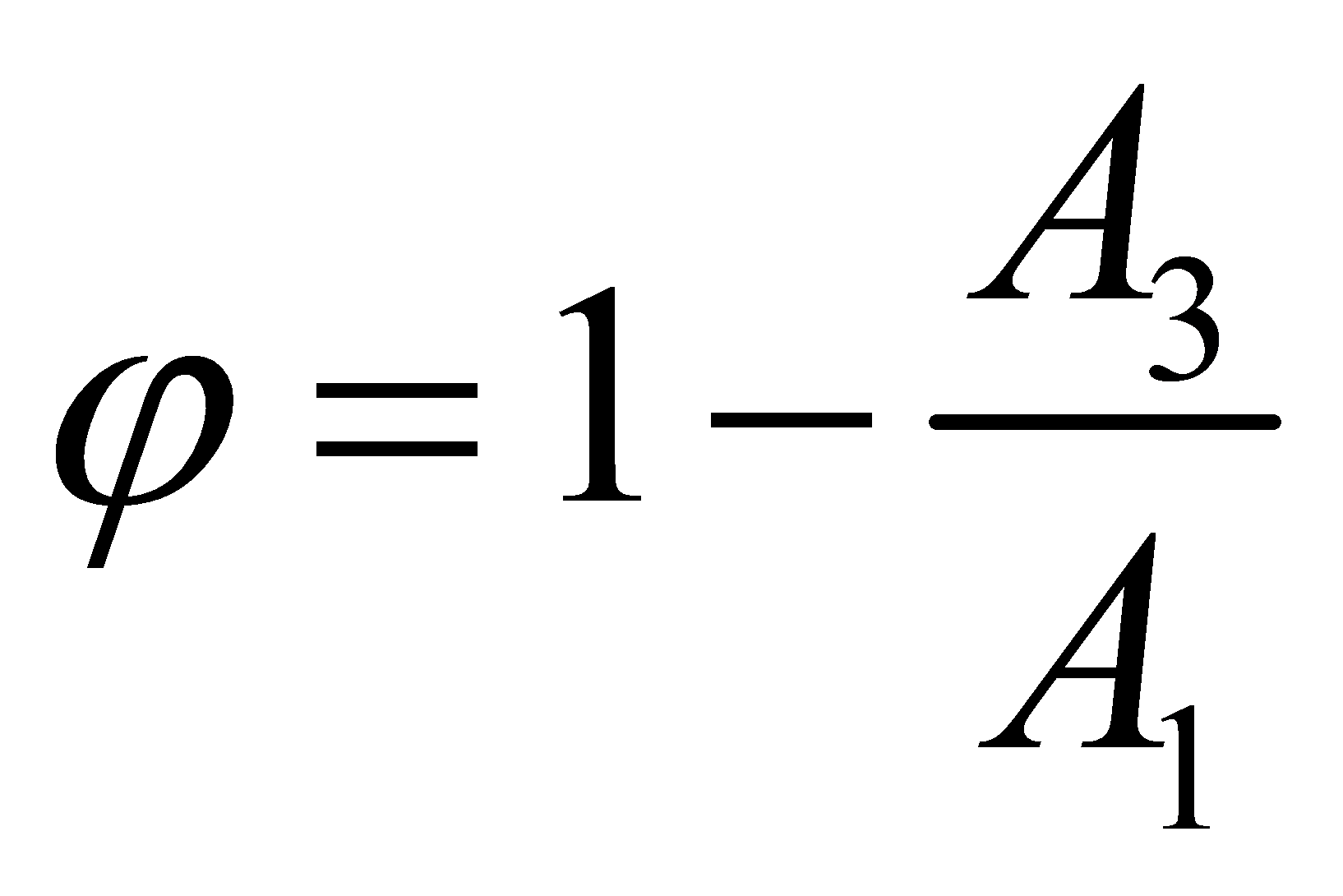 或衰減率
或衰減率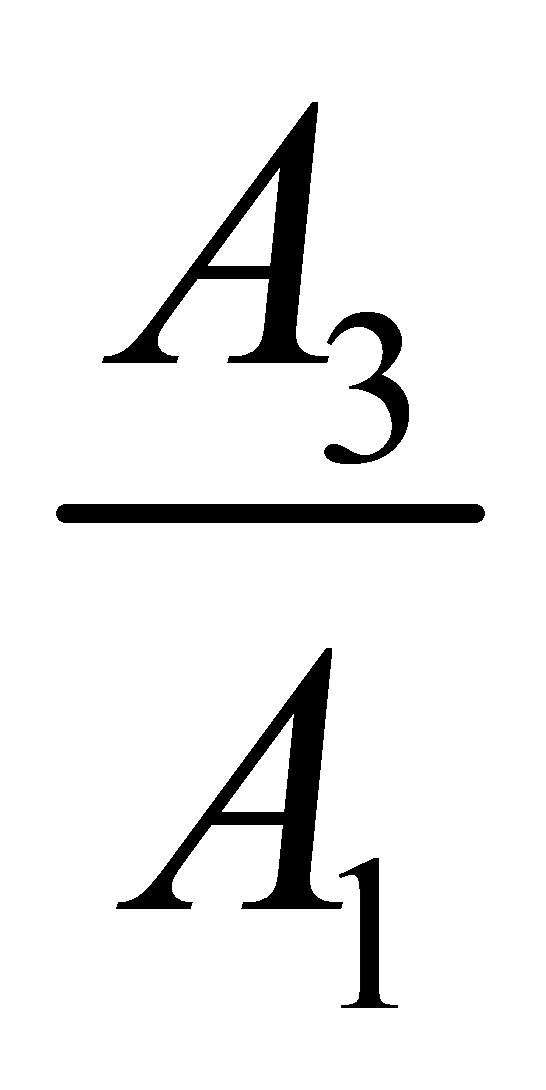 ;
;
(6)誤差平方積分值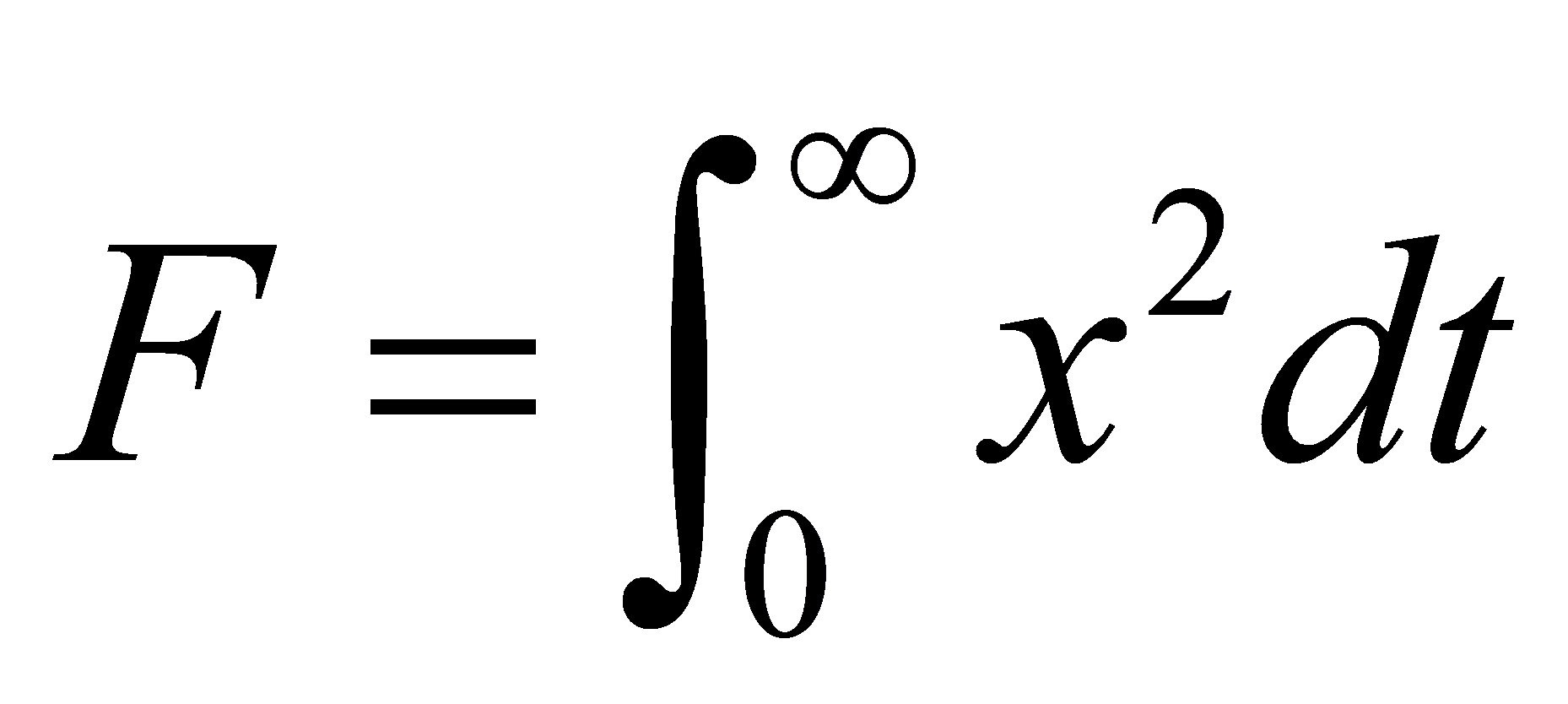
如果系統的上述項品質指標都不超過預先規定的限值,那末系統就具有所需的品質,或者說滿足給定的品質要求。
2.作為系統品質要求的過渡過程的典型形態有以下幾種:
(1)超調20%過程(σ%=20%);
(2)4:1衰減過程(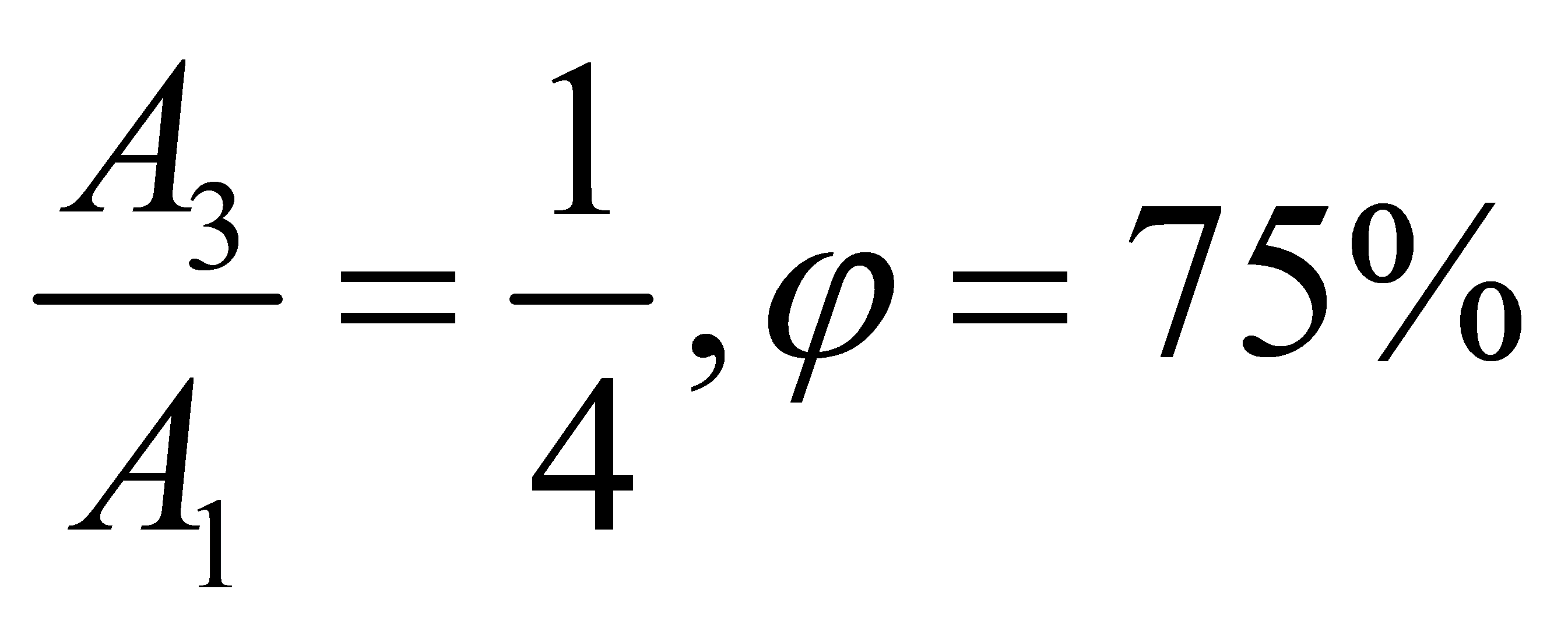 )
)
(3)10:1衰減過程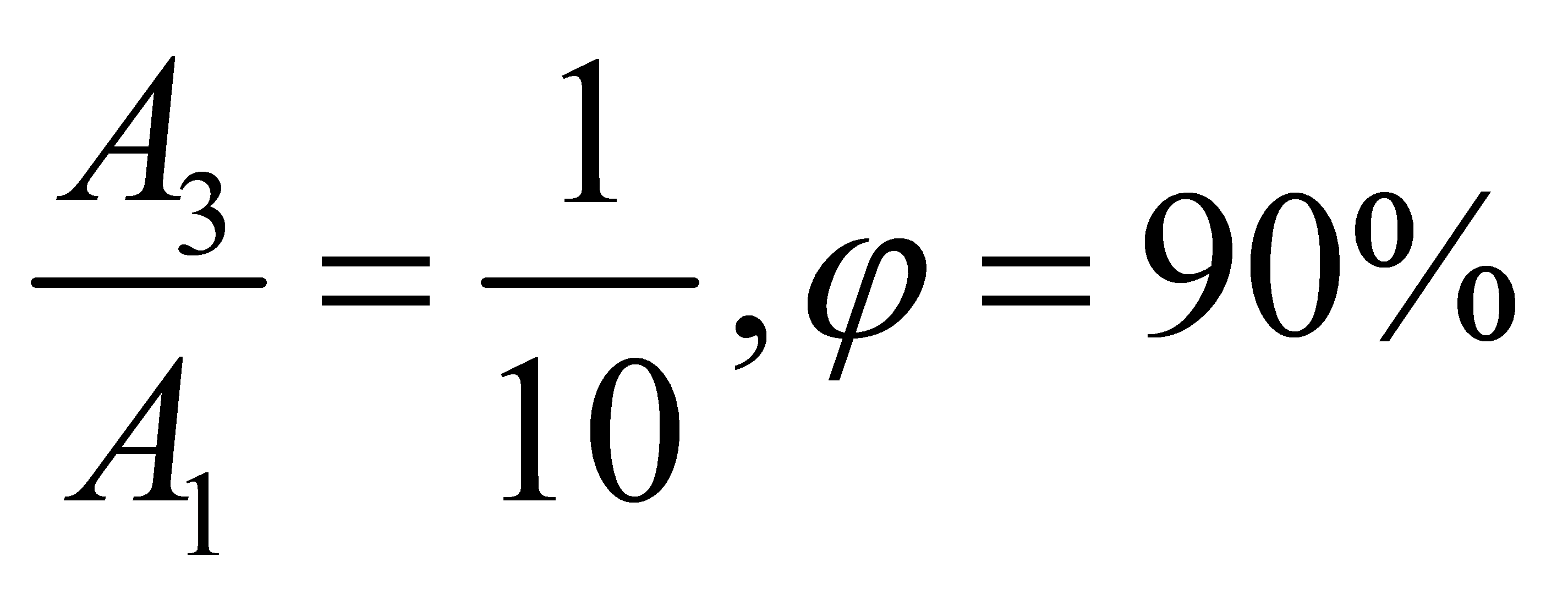
(4)調節時間最短過程(Tp最小);
(5)平方積分值最小過程(F最小);
(6)無超調過程(σ%=0)。
三.近代發展的幾種先進智能預測控制
(a)人工神經網絡PID控制
(b)遺傳法PID控制
(c)模糊PID控制
(d)專家控制
(e)免疫反饋機理控制
(f)網絡化控制
(g)模糊控制
隨著科學技術的發展,還會出現新的,更先進的整定方法。
戈 劍
2019.1.15整理